Merge Sort Python Tutorial - An Efficient Way Of Sorting

Welcome to Merge Sort Python Tutorial. In this tutorial, you will learn a very important topic of data structure that is Merge sort. Here i will cover these topics – merge sort introduction, algorithm, implementation, complexity, applications and some other concept. So let’s start merge sort in python.

We have many sorting techniques like Insertion sort, Bubble sort, selection sort. But these techniques are poor. It means, for example, for a given n which is equal to 1000 (n=1000= 10³), the algorithm will take n ²iterations that is 10⁶

But suppose you are given a data which is more than 10³ , let say 10⁵ then your algorithm will take 10¹⁰ iterations. These algorithms will take lots of time to execute, so now time to discuss something well. So i am going to discuss a very important sorting algorithm which is also often used algorithm, which is called merge algorithm. So let’s start Merge Sort Python Tutorial.

Merge Sort Python Tutorial – A Very Fast Sorting Method

What is Merge Sort ?

Merge sort based on Divide and Conquer approach.
That means it divides the array into two parts, those sub-arrays will be divided into other two equal parts. We will divide the array in this manner until we get single element in each part because single element is already sorted. After completion of dividing array, its time to conquer or merge them together but in sorted manner. Hence we get a sorted array.
Merge sort is recursive(method that call itself).
Very efficient for large data set.

How Merge Sort Works ?

In this section you will learn, how merge sort works.

Conceptually, Merge sort works in following manner.

Divide an unsorted array into two subarrays, and repeat dividing subarrays into further subarrays until you get single element in each part or sub-array.
Merge these subarrays in the same way as had divided it, but in sorted manner. This process will repeated until there is only 1 subarray remaining. This will be your sorted array.

Let’s understand it with an example –

Let’s consider we have an array [2,6,1,4]

Dividing

Step 1 : Now we will divide this array into two subarrays

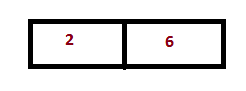
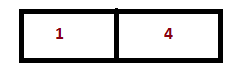
Step 2: Now we will divide these subarrays into further subarrays

Now we have only one element in each subarray, so it’s time to merge them. We have to merge them in the same manner as had divided it, but in sorted manner.

Step 3: Compare 2 with 6 and 1 with 4 , and place them in sorted order.

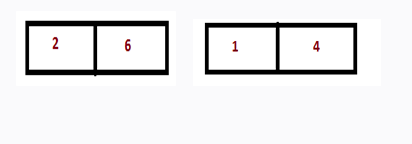
Step 3: Now we have to compare the above two sorted subarrays and sort them.

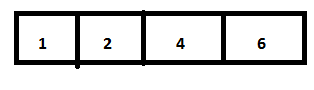
This is our sorted array. In this way you can sort a large data using merge sort method.

Merge Sort Algorithm

Now we will see merge sort algorithm. Merge sort takes place in two parts – first one is dividing array into subarrays and then merging them in sorted order. So we will see it one by one.

Dividing array into subarrays

Mergesort(Array)

Step : 1


set n = length(Array)

If (n<2) then return

set n = length(Array)

If (n<2) then return

Step : 2


set mid = n/2

Initialize array “left” having size (mid)

Initialize array “right” having size (n-mid)

set mid = n/2

Initialize array “left” having size (mid)

Initialize array “right” having size (n-mid)

Step : 3


for i = 0 to mid – 1

left [i] = Array[i]

[exit loop]

               for i = mid to n-1

right[i] = Array[i]

[exit loop]

for i = 0 to mid – 1

left [i] = Array[i]

[exit loop]

for i = mid to n-1

right[i] = Array[i]

[exit loop]

Step : 4


call mergesort(left)

Call mergesort(right)

Call merge(left,right,Array)

call mergesort(left)

Call mergesort(right)

Call merge(left,right,Array)

Merging Subarrays

merge(left, right, Array)

Step : 1


 set i = 0, j =0,  k = 0

[i,j,k will represent the indexes of left,right and Array respectively. ]

set i = 0, j =0, k = 0

[i,j,k will represent the indexes of left,right and Array respectively. ]

Step : 2


while (i<length(left) and j<length(right)

{

If (left[i] < right[j])

Then set Array[k] = left[i]

Increase i by 1

[end of if statement]

else

Set Array[k] = right[j]

Increase j  by 1

[end of else statement]

Increase  k by 1

[end of while loop]

while (i<length(left) and j<length(right)

{

If (left[i] < right[j])

Then set Array[k] = left[i]

Increase i by 1

[end of if statement]

else

Set Array[k] = right[j]

Increase j by 1

[end of else statement]

Increase k by 1

[end of while loop]

Step : 3


while (i < length(left))

{

Set Array[k] = left[i]

i = i + 1

k = k + 1

}

While (j < length(right))

{

Array[k] = Right[j]

Increase j by 1

Increase k by 1

}

while (i < length(left))

{

Set Array[k] = left[i]

i = i + 1

k = k + 1

}

While (j < length(right))

{

Array[k] = Right[j]

Increase j by 1

Increase k by 1

}

Merge Sort Python Example

Now we will see, how to implement merge sort in python practically.

The code of merge sort have two parts. So let’s start,


# Define definition for merge which basically takes two arrays i.e., the left and right part
def merge(left, right):
    result = []  # final result array, that is an empty array

#create two indices and initialize with 0
    i,j = 0,0

# Till this condition is true, keep on appending elements into resultant array
    while i<len(left) and j<len(right):
        if left[i] <= right[j]:
            result.append(left[i]) #append ith element of left into resultant array
            i+=1
        else:
            result.append(right[j])  #append jth element of right into resultant array
            j+=1

# it is basically specifies that if any element is remaining in the left array from -
# ith to the last index so that it should appended into the resultant array. And similar -
# to the right array.
    result += left[i:]
    result += right[j:]
    return result

# Definition for merge sort
# this takes an input list
def mergesort(lst):
    if(len(lst)<= 1): # this means that the list is already sorted.
        return lst
    mid = int(len(lst)/2)

# left array will be mergesort applied over the list from starting index 
# till the mid index
    left = mergesort(lst[:mid])

# right array will be mergesort applied recursively over the list from mid index
# till the last index 
    right = mergesort(lst[mid:])

    return merge(left,right)  # finally return merge over left and right

# create an array, assign elements into it  
arr = [1,9,4,3,2]
print(mergesort(arr)) # print sorted array

# Define definition for merge which basically takes two arrays i.e., the left and right part

def merge(left, right):

result = [] # final result array, that is an empty array

#create two indices and initialize with 0

i,j = 0,0

# Till this condition is true, keep on appending elements into resultant array

while i<len(left) and j<len(right):

if left[i] <= right[j]:

result.append(left[i]) #append ith element of left into resultant array

i+=1

else:

result.append(right[j]) #append jth element of right into resultant array

j+=1

# it is basically specifies that if any element is remaining in the left array from -

# ith to the last index so that it should appended into the resultant array. And similar -

# to the right array.

result += left[i:]

result += right[j:]

return result

# Definition for merge sort

# this takes an input list

def mergesort(lst):

if(len(lst)<= 1): # this means that the list is already sorted.

return lst

mid = int(len(lst)/2)

# left array will be mergesort applied over the list from starting index

# till the mid index

left = mergesort(lst[:mid])

# right array will be mergesort applied recursively over the list from mid index

# till the last index

right = mergesort(lst[mid:])

return merge(left,right) # finally return merge over left and right

# create an array, assign elements into it

arr = [1,9,4,3,2]

print(mergesort(arr)) # print sorted array

merge(left, right) basically merges two arrays that is left array and right array and gives us the resultant array, which is basically sorted.

So the result of merge sort is following –

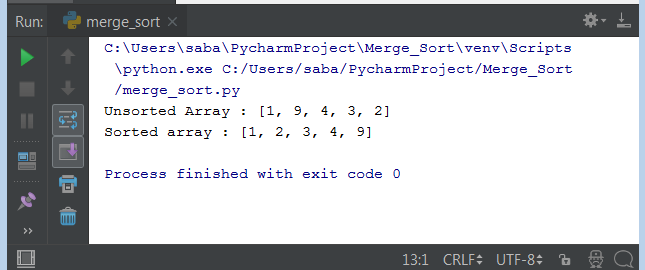
Merge Sort – Big Oh Analysis

Merge sort does log n merge steps because each merge step double the list size.
It does n work for each merge step because it must look at every item.
So it runs on O(n log n).

Merits Of Merge Sort

Merge sort can be applied to any file size.
Merge Sort is useful for sorting linked lists.
It is always fast even in worst case, its runtime is O(n log n).
It is stable sort which means that the same element in an array maintain their original positions with respect to each other.

Demerits Of Merge Sort

It requires additional memory to sort the elements.
Recursive calls result in additional overhead making it unsuitable for small number of elements.

Merge Sort Python Tutorial – An Efficient Way Of Sorting